Understand the dreaded recursion in 7 minutes

Whether you are struggling with recursion in your computer science class or you are a programmer who has never really appreciated the concept of recursion, you have come to the right place. Recursion is broken down for you in this article, and you should be able to write a recursive procedure after reading it.

Intro

Imagine you are in a large auditorium and you are seated in the last row and you want to answer the question: how many rows are in the auditorium? To do so, you need to know the number of rows in front of you. So, you ask the person in front of you the same question (how many rows are in front of them?), and they, in turn, ask the person in front of them the same question.

When the question eventually arrives at the first row, the person in the first row will tell the person in the second row that there are zero rows in front of them. The person in the second row will tell the person in the third that there's one row in front of them. This will go on until the answer gets back to you.

This procedure of counting rows can be broken down into 3 steps:

1. State the problem (how many rows are in the auditorium?)

2. Solve smaller instances of the same problem (how many rows are in front of the subsequent rows)

3. Finally, stop when the base case is satisfied i.e. (when there are no more rows to count)

This watered-down example is similar to how recursion works in computer programs (A function repeatedly calls itself until some condition is satisfied).

What is recursion

Recursion is a programming technique where a function repeatedly invokes (calls) itself until some condition is satisfied.

It sounds silly, yes! But how does a function or procedure call itself?

Looking back to the auditorium analogy above, the question of how many rows we asked the audience is a recursive procedure because it has to call itself continuously until there are no more rows to count. This happens like this:

Let's assume there were 3 rows in the auditorium but we did not know that, this is how we can find out recursively:

1. Starting from the 3rd row, you ask the person in your front: how many rows are in front of you? (person answers: "2rows")

2. The person in the 2nd row calls the same procedure(question) again how many rows are in front of you? (person answers "1 row")

3. The 3rd person asks the same question again. This time however the answer is 0. Hence, the question (procedure) stops here.

4. Finally, the third person tells the second that there are 0 rows in front of them, the second person answers that there is 1 row in front of them, and you answer that there are 2 rows in front of you.

Implementing recursion

A recursive procedure consists of 2 significant cases which are:

1. Base case: The base case is the condition for which a recursion should end. It's also the instance for which a problem has a solution that does not depend on recursion.

2. Recursive case: This is where our recursive procedure calls itself.

Example: Write a recursive function that computes the factorial of a number.

Before solving this problem, we need to know what the factorial of a number is.

The factorial of a number is the product of the number and every whole number between 1 and itself.

Mathematically, n! = n * (n-1) * (n-2) * (n-3) * ... * 1

So, 5! = 5 * 4 * 3 * 2 * 1, 3! = 3 * 2 * 1 and so on...

The following is a function that computes the factorial of a given number.

function computeFactorial(n) {
  if (n == 0) return 1;  // base case

return n * computeFactorial(n-1); // recursive case
}

//logs: 120

In the function above, we are telling the computer two things:

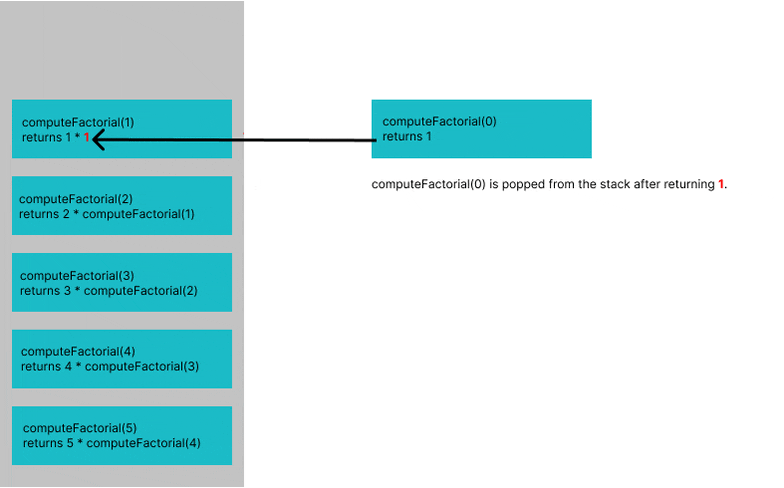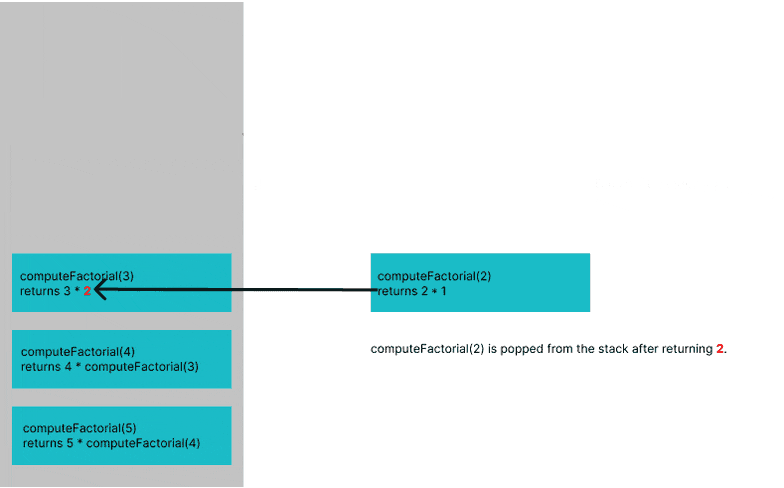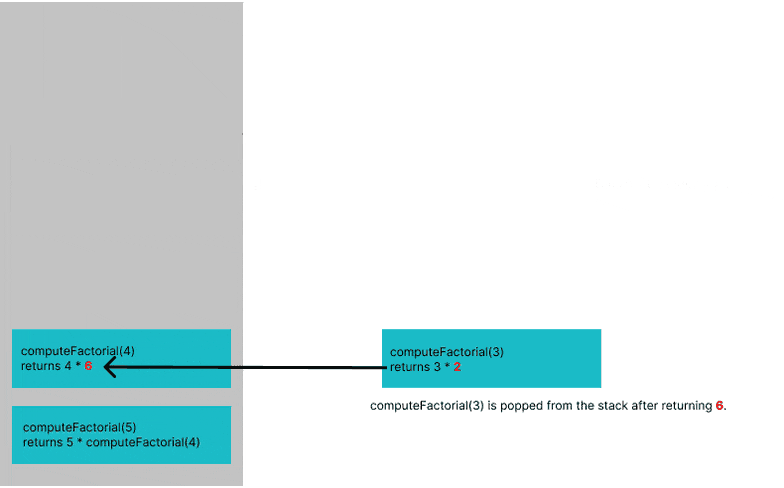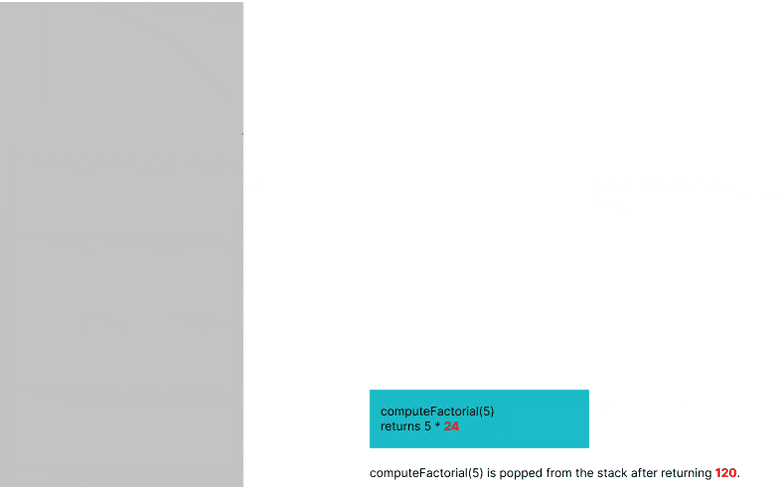
1. Terminate the recursive call when the base case is satisfied (i.e. when n equals 0 because we know that the factorial of 0 is 1).

2. Continue calling computeFactorial with lesser values (n-1), (n-2) ... until the base case is satisfied.

   Note that each subsequent call will go through the if statement until the base case is satisfied.

3. The number which satisfies this condition for our factorial function above is computeFactorial(0). The function will terminate after this call.

Important: Always specify a base case for a recursive procedure to prevent an endless recursive call.

More on recursion

To fully appreciate the concept of recursion, you should be familiar with the following terms:

• stack

• stack frame

• and call stack

Stack: A stack is a data structure that stores data in a LIFO (Last In First Out) order. LIFO means that the last item pushed (added) into the stack will be the first item to be popped (removed) from the stack.

Call stack: The call stack contains all the information about a function (the local variables of the function, return values, and function calls inside the current function). The call stack is implemented with a stack data structure.

Stack frame: A stack frame is a single item in the stack. If a stack is a bunch of plates placed on top of one another, then a stack frame represents each plate. Each frame gets removed from the stack after the function associated with it is executed. Refer to the image below for clarity.

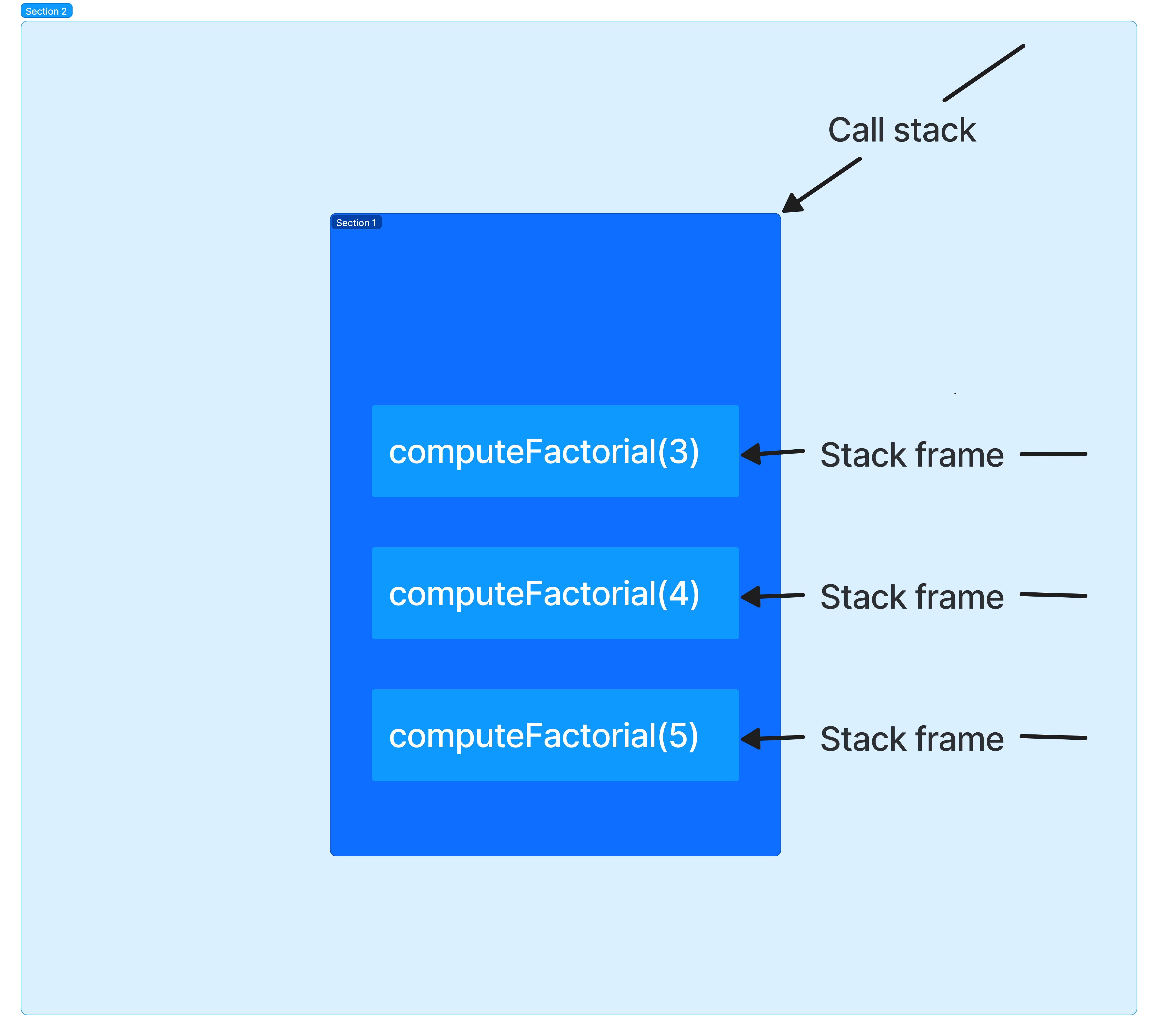
Stack overflow: A stack overflow results when the size of the stack frames exceeds the size of the call stack. This usually happens when there are too many function calls inside the stack.

Checkpoint

The following question is adapted from FreeCodeCamp's JavaScript and Algorithms and Data Structures curriculum.

Write a recursive function that returns the sum of the numbers in an array

Write a recursive function, sum(arr, n), which returns the sum of the first n elements of an array arr.

function sum(arr, n) {

}
//hint: start by writing the base case

sum([5,5,10,10,20],3) // it should return 20

See the solution below:

function sum(arr, n) {
  if (n <= 0) return 0;
  return arr[ n - 1] + sum(arr,n-1)
}

console.log(sum([50,20,30], 2)) // returns 70

The base case returns 0 if the number specified is less than or equal to 0

The recursive case returns the sum of the first n numbers in the array. We use arr[n -1] above because arrays are zero-indexed; hence we subtract 1 to accommodate for this.

For example, sum([20, 30 40], 2) works like this:

• Starting from the next-to-last number, we have arr[2-1] + arr[2-2] which evaluates to arr[1] + arr[0] as required.

Conclusion

Recursion can be tough to grasp initially but it becomes intuitive when you learn to think recursively. Remember that everything you can do with recursion, you can do with loops and loops should be preferred over recursion for clarity and readability.

Thanks for reading! See you next time